📍행렬과 벡터
m * n 행렬 형태
- m: 행(row)
- n: 열(column)
- 벡터도 행렬이다 (예 1 * 2 행렬, 1 * 3 행렬)
row vector
- 2D 벡터: (x, y)
- 3D 벡터: (x, y, z)
column vector
(x
y
z)
- vector의 곱셈은 행렬의 곱셈과 같다
행렬 전치(transpose)

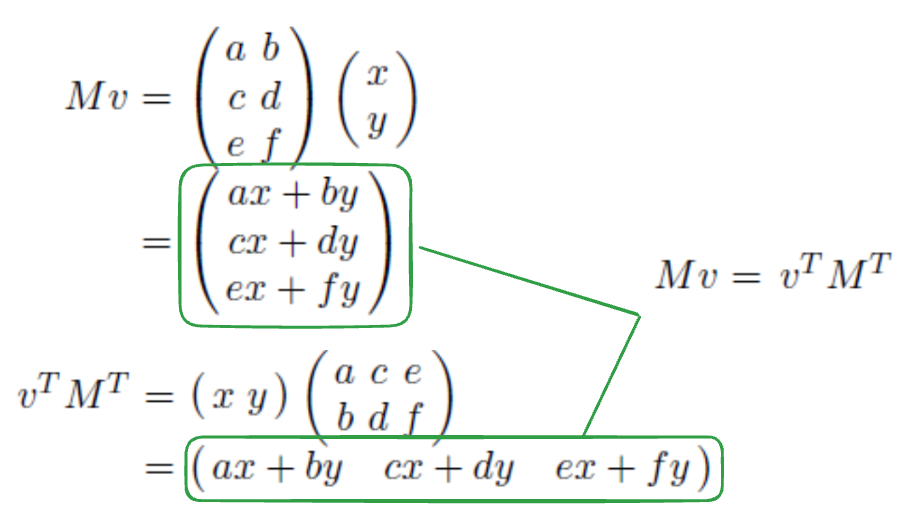
행렬 곱셈 M * v 는 vt * Mt 와 같다
- 조건

- 곱셈 결과
OpenGL의 곱셈 방식
- column vector 사용하므로, 행렬벡터 곱셈 시, 벡터가 행렬 뒤에서 곱해짐
- 참고로 Direct 3D는 row vector 사용하므로 반대
단위 행렬과 특징

행렬곱셈의 역행렬과 전치행렬

벡터의 크기(길이)
- 원점에서의 거리

- 벡터를 벡터의 길이로 나누는 과정을 정규화(normalization)이라고 함
- 정규화된 벡터는 항상 길이가 1이며, 단위 벡터라고 함
📍좌표계
좌표계(coordinate system) = 원점(origin) + 기저(basis)
- 기저: (1, 0), (0, 1) 처럼 기본이 되는 벡터. 조합하여 더 큰 벡터를 만들 수 있음(선형 조합: linear combination)
- orthonormal: orthogonal(직교) + normalized 벡터
예) (0, 1), (1, 0) -> x, y 축 나란히 직교
예) (-1 / 루트2, 1 / 루트2), (1 / 루트2, 1 / 루트2) -> y축 기준으로 45도 기울어져서 직교)
- standard: 기저 벡터
예) (0, 1), (1, 0)
3차원에서는 x, y, z 축에서 다시 생각
📍Dot Product(Inner Product = 벡터의 내적)
- 2개의 2차원 벡터 a(a1, a2), b(b1, b2)가 주어졌을 때
- 벡터의 내적 = a1 * b1 + a2 * b2
- 3차원 벡터일 경우에도 같은 방식으로 계산
또한 벡터의 내적(a*b)에 아래 공식이 성립(대수적 정의와 기하학적 정의)

- 자기 자신과의 내적은 항상 1
- orthonormal한 벡터끼리의 내적은 항상 0
📍Cross Product(벡터곱)

- 3차원 벡터에서만 다뤄짐
- 3차원 벡터 a, b 가 있을 때, 벡터곱을 a x b 형태로 표시할 수 있다
- a×b의 길이는 a와 b가 걸쳐 있는 평행 사변형의 면적과 같다
- a = b 일 때, axb = 0
- 또한 오른손 법칙에 따라 bxa = -axb 가 성립
- 벡터곱 결과의 좌표 구하기

📍Line, Ray, Linear Interpolation
두 점 p0, p1 을 잇는 무한한 직선을 아래처럼 표현할 수 있다
- 선형 보간(linear interpolation)을 통해 p0과 p1 사이의 점 p(t)을 구할 수 있다.
- p(t) 는 가중치가 부여된 p0 + p1

t 범위에 따른 p(t)
- Infinite line: 매개변수 t의 범위가 -무한대 ~ +무한대일 때: p(t)
- Ray: t가 0 ~ +무한대 일때 p(t)
- Line segment: t가 0 ~ 1일 때 p(t). p0 ~ p1의 선형 보간과 일치
3차원에서 선형 보간
- 아래처럼 color 형태로 표현 가능

참고
https://youtu.be/774mc7tC594?si=ulz_T7YHn2ElPCZS
